Disclaimer
The information contained in the website is solely intended for professional investors. Some funds shown on this website fall outside the scope of the Dutch Act on the Financial Supervision (Wet op het financieel toezicht) and therefore do not (need to) have a license from the Authority for the Financial Markets (AFM).
The funds shown on this website may not be available in your country. Please select your country website (top right corner) to view more information.
Neither information nor any opinion expressed on the website constitutes a solicitation, an offer or a recommendation to buy, sell or dispose of any investment, to engage in any other transaction or to provide any investment advice or service. An investment in a Robeco product should only be made after reading the related legal documents such as management regulations, prospectuses, annual and semi-annual reports, which can be all be obtained free of charge at this website and at the Robeco offices in each country where Robeco has a presence.
By clicking Proceed I confirm that I am a professional investor and that I have read, understood and accept the terms of use for this website.
Quantitative investing
Gradient descent
Gradient descent (GD) is the cornerstone of many optimization algorithms. It is used to find a local minimum of a differentiable function, taking steps proportional to the negative of the gradient of the function at the current point. GD is an iterative algorithm that improves its output step after step and can therefore be used to update the parameters of a model.
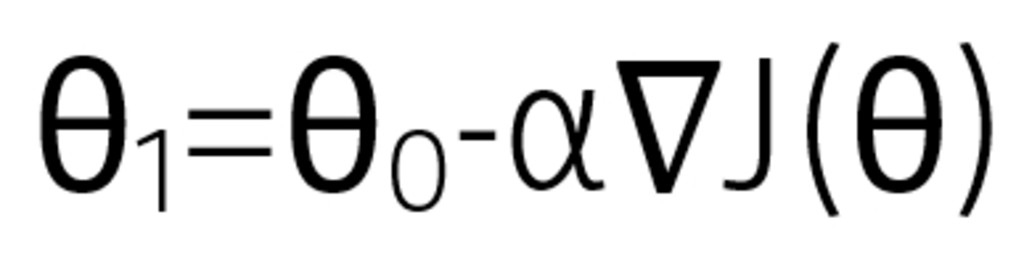
Where
θ0: current position
θ1: next position
α: small step (or step size)
∇J(θ): fastest direction increase
To use an analogy, imagine a hiker (the algorithm) lost atop a hill (the function) in foggy weather, trying to get down as quickly as possible. To avoid wasting time, the hiker needs to walk downwards in the direction where the slope is the steepest. The hiker has an instrument (the gradient) to assess steepness, but, this tool is not very handy and requires stopping each time to make the measurement. The hiker thus tries to limit using this tool.
At the start of the decent, the slope is very steep and hiker can walk long stretches (steps) without stopping for measurement. But as the destination gets closer, measurements become more frequent, to avoid missing the bottom. Using this method, the hiker eventually reaches the bottom (local minimum), assuming he or she avoids getting stuck in a local obstacle, like a mountain lake, for example.
GD is one of the most common techniques used in machine learning (ML). Some even argue ML is nothing more than GD on a function with thousands of parameters. ML is about using empirical data to refine a model – for example, an asset pricing model – to minimize discrepancies between model results and reality (the function), and then making predictions with the refined model.
Quantitative investment strategies increasingly involve analyzing large, complex and disparate datasets, that are difficult – or even impossible – to specify with traditional financial models, which rely on closed form solutions. In this context, ML methods, using tools such as GD, can turn out to be more useful than standard, widely used statistical techniques.
One example is the use of ML to analyze financial text data, such as regulatory filings, earnings releases or news articles. While the capacity of traditional techniques to extract relevant signals from text remains limited,1 interesting results regarding stock-price forecasting applying ML on financial news have been reported and represent a promising area for future research.
Next-generation quant
As technology advances, so do the opportunities for quantitative investors. By incorporating more data and leveraging advanced modelling techniques, we can develop deeper insights and enhance decision-making.
Footnote
1 These are mainly techniques based on bag-of-words, noun phrase and/or named entity feature extraction combined with manual feature selection. With these techniques, however, much of the structure of the text is lost.
