免责声明
荷宝私募基金管理(上海)有限公司及其关联公司(“荷宝”)授予您访问本网站的权利, 但您需遵守以下条款和条件。请您仔细阅读以下条款和条件。
访问本网站及其任何页面, 即表示您声明并保证您所在司法管辖区的适用法律和法规允许您访问该信息, 并且您已同意以下条款和条件。如果您不同意这些条款和条件, 请不要访问本网站。 荷宝保留更改该等条款和条件的权利, 您应当定期查看此类更改, 您继续使用本网站即表示同意所有此类更改。
本网站上的任何内容均不构成税务、会计、监管、法律、保险或投资建议。本网站所载的信息或任何意见均不构成荷宝对买卖任何证券、期货、期权、基金或其他金融工具的招揽或要约, 并且若在任何司法管辖区内, 根据其适用法律, 此类要约、招揽、购买或出售是违法的, 也不得向任何人提供或出售任何此类金融工具。
限制
本网站不针对由于任何原因本网站被禁止发布或使用的司法管辖区内的人士, 任何适用此类禁令的人士不得访问本网站。访问本网站的用户有责任遵守适用法律法规。
信息与材料
这些页面中包含的信息, 材料, 条款, 条件和说明可能会有所变化。本网站包含的信息和材料, 包括但不限于文本, 图形, 链接或其他项目, 均为“现有”或“现存”信息。
荷宝尽合理努力在本网站中提供准确和最新的信息。但是荷宝不保证此信息和材料的准确性, 充分性或完整性, 并明确表示不对此类信息和材料中的错误或遗漏承担责任。您必须自己评估本网站所含信息的相关性, 准确性和充分性, 并进行您认为必要或适当的独立调查, 以进行此类评估。本网站包含的任何意见或估计均为一般性的, 您不得依赖其作为建议。
荷宝及其任何雇员或代理均未对您或任何特定人士或群体的投资目标, 财务状况或特殊需要进行任何考虑或调查。因此, 对于因您或任何人士或群体根据本网站包含的任何信息, 意见或估价而直接或间接造成的任何损失, 荷宝不作任何保证, 也不承担任何责任。
用于编制本网站的任何研究或分析均由荷宝获得, 供其自行使用, 并且可能是出于其自身目的而采取的行动。荷宝保留随时更改和更正意见、本网站及相关材料和链接的权利, 恕不另行通知。
不保证: 限制与责任
荷宝提供本网站的信息及材料, 但不作出与此相关的任何保证, 无论是明示的, 暗示的或法定的保证, 包括但不限于不侵犯第三方权利, 所有权, 适销性, 适用于特殊用途, 或免于计算机病毒的保证。
对于通过使用或访问本网站可能导致的任何形式的损失或损害, 包括直接的、间接的或后果性的损害, 荷宝均不承担责任。
互联网用户应该意识到, 由于我们无法控制的情况,
互联网上的通信可能会受到干扰、传输中断、数据传输延迟或错误的影响。荷宝明确表示不对中断、缺陷、操作或传输延迟、计算机病毒或系统故障,
或与本网站提供的信息和材料中的任何错误或遗漏承担责任。此外, 对于与本网站、使用或无法使用本网站有关或由此引起的任何损失或损害,
或任何未经授权方和任何计算机病毒篡改用户计算机系统的行为, 荷宝均不承担责任。
Quantitative investing
Shapley values
Shapley values are a concept borrowed from game theory. Regarding the latter, the game constitutes a setting in which players contribute to an overall outcome (payoff). In terms of this, Shapley values are used to distribute the gains or costs fairly across several players cooperating in coalitions. Effectively, they are the average marginal contributions (gains or costs) for all players, when all possible coalitions have been taken into account.
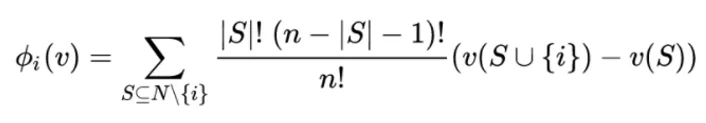
Where
φi is the Shapley value for player i
N is the set of all players and N\{i} is the set of all players excluding player i
n is the number of players in set N: the total number of all players
S is any subset of the set of all players excluding player i
v(S) is the payoff for a coalition consisting of the players in set S
For example, take two individuals (A and B) who would like to Uber home after work. If they do so separately, the cost for A is EUR 10 and for B EUR 15 given varying distances. However, if they share the ride, the fare amounts to EUR 20. With Shapley values, you can calculate how this should be split fairly between the two individuals. In this scenario, the players (A and B) form a coalition (carpool) and they play a game (Uber ride) to obtain a payoff/cost (EUR 20 fare).
In this setting, the Shapley values amount to the players’ average marginal contributions (or costs) across all possible orders in which the players can join the carpool arrangement, i.e., if A hails the ride first or if B is the first to request it. If A books the Uber, her marginal contribution will be EUR 10. Given that B joins the carpool as the second individual, his contribution will also be EUR 10 as that the total cost of the ride is EUR 20. But if B hails the ride, his marginal contribution will be EUR 15 and A will contribute the remaining EUR 5. Therefore, the Shapley values would then amount to EUR 7.5 for A – (10+5)/2 – and EUR 12.5 for B – (10+15)/2.
Shapley values have many applications, including machine learning (ML). In terms of our quant investing platform, we use them in interpreting our ML models. For example, they can help us to determine which variables (features) are the most impactful in our models and rank them in terms of importance. They can also shed light on the outputs generated by our models by deconstructing the marginal contributions of features, thus allowing us to better understand the economic rationale behind our model predictions.