LASSO is an acronym that stands for ‘least absolute shrinkage and selection operator’. It is associated with a machine learning technique – LASSO regression – that performs both shrinkage and variable selection to simplify linear regression models and prevent overfitting.
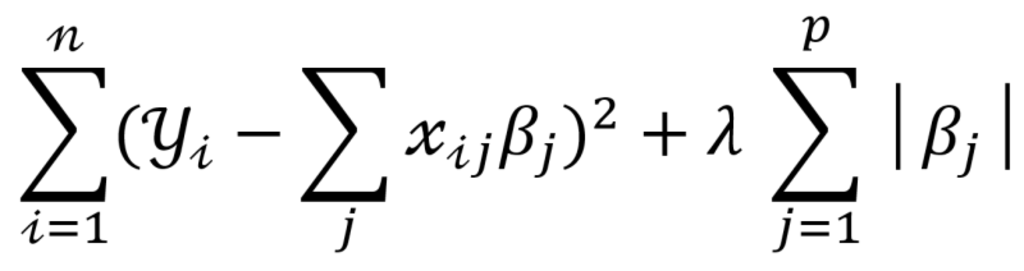
Where
λ is amount of shrinkage or penalty
λ = 0 implies all features are considered as no parameters are eliminated
λ = ∞ implies no feature is considered
A linear regression allows you to determine if there is a relationship between variables. For example, it can quantify the relationship between a dependent variable (crop yields) and explanatory variables (soil fertility,temperature, water quality, etc.). But in cases where there are many candidate variables to explain crop yields, the statistical model can become complex and difficult to process.
The LASSO regression is helpful in such instances as it can select variables based on their importance. This is achieved through a process called shrinkage, a method which imposes a penalty to reduce the absolute size of the regression coefficients. Although reduced in magnitude, the most important variables will continue to reflect material coefficients, while the less-contributing variables will exhibit values close to zero or even zero.
Through this process, it identifies which variables to keep and which ones to exclude, based on the size of their coefficients. Using our example, the technique would gradually select the variables which best predict crop yields, beginning with the most important one before working its way through the list. At some point, adding more variables would no longer improve the prediction accuracy of the model sufficiently, but instead it would add substantial complexity.
Therefore, the technique allows you to simplify a model by reducing the number of parameters in a regression and precluding potential data noise. It also enables you to guard against overfitting by eliminating variables with little explanatory power, potentially making the model more robust across different datasets. Additionally, it can help optimize models with high multicollinearity as it can choose between correlated explanatory variables.
In general, the LASSO regression is a basic machine learning (ML) technique that can be used for many applications. It is essentially a standard linear regression with a slight twist. Contrary to more sophisticated ML techniques, however, it is not able to pick up non-linear relationships between variables.
For our quant investing platform, it has the potential to help fine-tune models by assisting us with variable selection. For instance, we have used it to select company characteristics that have linear predictive value for risk and returns. We have also used it to identify which industries lead or lag others in terms of returns.





















